总算进入我们的排序相关算法的学习了。相信不管是系统学习过的还是没有系统学习过算法的朋友都会听说过许多非常出名的排序算法,当然,我们今天入门的内容并不是直接先从最常见的那个算法说起,而是按照一定的规则一个一个的介绍。
首先,我们要介绍的排序算法是插入类型的排序算法。顾名思义,插入排序就是将无序的一个或几个记录“插入”到有序的序列中,比较典型的例子就是简单插入排序和希尔排序。
简单插入排序
简单插入排序,也可以叫做直接插入排序。还是先看代码,再来进行下一步的解释。
function InsertSort($arr)
{
$n = count($arr);
for ($i = 1; $i < $n; $i++) { // 开始循环,从第二个元素开始,下标为 1 的
$tmp = $arr[$i]; // 取出未排序序列第一个元素
for ($j = $i; $j > 0 && $arr[$j - 1] > $tmp; $j--) { // 判断从当前下标开始向前判断,如果前一个比当前元素大
$arr[$j] = $arr[$j - 1]; // 依次移动元素
}
// 将元素放到合适的位置
$arr[$j] = $tmp;
}
echo implode(', ', $arr), PHP_EOL;
}
InsertSort($numbers);
// 49, 38, 65, 97, 76, 13, 27, 49
// 13, 27, 38, 49, 49, 65, 76, 97代码量不多吧,其实也非常好理解。我们就拿测试数据的前两个数来简单地说明一下。
首先,第一个循环是从 1 开始的,也就是说,第一个取出的未排序序列元素是 tmp = arr[1] ,也就是当前的 tmp = 38 。
然后开始循环,当前的循环是判断 j-1 的元素是否比当前这个 tmp 元素大,如果是的话,进入循环体,arr[1] = arr[0] 。到目前为止,arr[0] 和 arr[1] 现在都是 49 。整个序列是 49,49,65,……
最后让 arr[0] = $tmp ,也就是等于 38 。(循环的时候 j– 了)。整个序列是 38,49,65,……
通过下面这张图片,我们可以更清楚地看明白整个序列完成排序的过程。
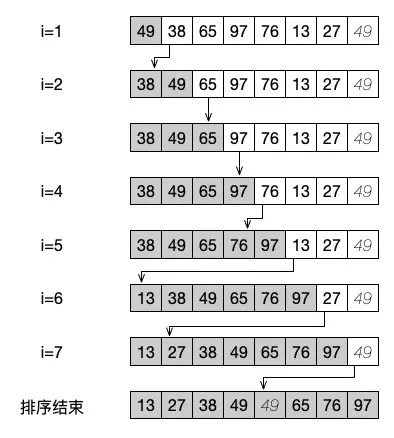
从上面的步骤可以看出,简单插入排序就是从一边开始,先让前面的数据逐步有序的过程。从代码中就可以看出,它是不断地内部地循环中进行 j 的递减,与前面有序的数列进行比对,当发现了自己合适的位置之后,就将数据放到这个位置上。
从代码和我们的分析来看,简单插入排序的时间复杂度是 O(n) 。同时,它是属于稳定的排序,什么叫稳定排序呢?细心的同学应该发现了,在我们的测试代码中,有两个相同的数据,也就是 49 。稳定的意思就是相同的数据在排序前后的位置不会发生改变,前面的 49 依然是在后面的 49 前面。这就是排序的稳定性。
另外,简单插入排序比较适合初始记录基本有序的情况,当初始记录无序,n 较大时,这个算法的时间复杂度会比较高,不太适合采用。
希尔排序
简单插入排序很好理解吧,希尔排序又是什么鬼呢?别着急,从这个名字我们是看不出什么端倪的,因为这个排序的名字是以它的发现者命名的。实际上,希尔排序还是一个插入排序的算法。
上文中说过,简单插入排序适合基本有序的情况,而希尔排序就是为了提升简单插入排序的效率而出现的,它主要目的是减少排序的 n 的大小以及通过几次排序就让数据形成基本有序的格式。
对于这个算法,我们不能先上代码了,先来看图吧。
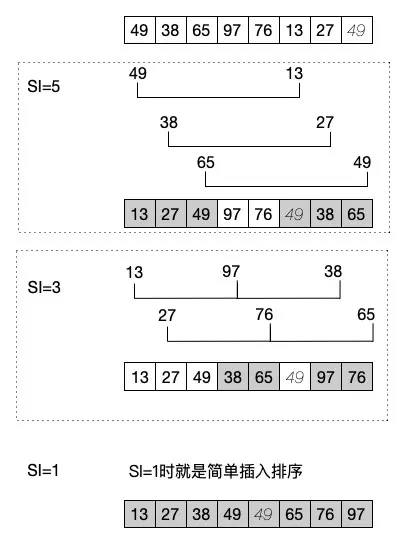
看明白了吗?我们其实是将数据进行分组了,每次分组是以一定的增量为基础的,比如我们这个示意图中就是第一次以 5 为增量进行排序,第二次是以 3 为增量。这样第三次排序的时候,增量为 1 ,也就成为一个普通的简单插入排序了。一会我们代码中就会体现出来。
还是按增量为迭代次序进行这三趟排序的具体分析吧:
1)第一次迭代的时候,我们将分组增量设置为 5 ,这时分别有三组数据,也就是 49 和 13,38 和 27,65 和 49 ,然后对这三组数据进行简单插入排序,之后的数组结果是 13、27、49、97、76、49、38、65 。
2)第二次迭代,分组增量为 3,这时就分成了两组,每组三个数据,分别是 13、97、38 为一组,另一组是 27 、76 、65 。对这两组数据进行简单插入排序之后更新数组结果为 13、27、49、38、65、49、97、76 。
3)其实从两次分组排序之后就可以看出,这个数组已经基本有序了。这时最后就是以分组增量 1 再次进行简单插入排序。说白了,最后这一步就是一个普通的简单插入排序的过程了。
分步骤讲解之后是不是清楚很多了,再重复一篇,希尔排序其实就是按分组来一次大范围的插入排序,最后一步步缩小到只有 1 次增量的简单插入排序了。我们再来看看代码吧:
function ShellSort($arr)
{
$n = count($arr);
$sedgewick = [5, 3, 1];
// 初始的增量值不能超过待排序列的长度
for ($si = 0; $sedgewick[$si] >= $n; $si++);
// 开始分组循环,依次按照 5 、3 、 1 进行分组
for ($d = $sedgewick[$si]; $d > 0; $d = $sedgewick[++$si]) {
// 获取当前的分组数量
for ($p = $d; $p < $n; $p++) {
$tmp = $arr[$p];
// 插入排序开始,在当前组内
for ($i = $p; $i >= $d && $arr[$i - $d] > $tmp; $i -= $d) {
$arr[$i] = $arr[$i - $d];
}
$arr[$i] = $tmp;
}
}
echo implode(', ', $arr), PHP_EOL;
}
ShellSort($numbers);看着代码貌似有三层 for 循环呀,它哪里提升了效率了呢?其实希尔排序的效率提升确实是有限的,它其实是通过前几次的分组让数据先基本有序。而在分组的状态中,数据比较的数量并不会达到 n 的级别。当最后一次进行简单排序的时候,整个数据已经是基本有序了,在这种情况下交换的次数明显也会减少很多,所以它的时间复杂度在理想状态下可以减少到 O(log2n) 的水平。
希尔排序是插入排序的一种改进版本,也称作”缩小增量排序”。它通过将原本的数据按照一定的间隔(增量)进行分组,对每一组分别进行插入排序,随着增量的逐渐减小,每组包含的元素越来越多,整个序列也逐渐变得有序,直到增量为1时,进行一次直接插入排序,完成整个排序过程。
算法原理
- 增量序列选择:
- 该代码使用了Sedgewick增量序列
[5, 3, 1]。- 增量序列决定了每次分组的间隔大小。
- 调整初始增量:
phpfor ($si = 0; $sedgewick[$si] >= $n; $si++);
- 这一步是为了确保初始增量不超过数组长度 n。
- 对于长度为5的数组
[5, 4, 3, 2, 1],初始增量会从5开始检查,由于5不小于数组长度5,所以$si保持为0,初始增量$d为$sedgewick[0]即5。- 但是,由于数组长度为5,增量为5时实际上只有一个分组(每个元素自成一组),没有比较的意义。因此,代码中的循环会继续,使得
$si变为1,初始增量$d变为$sedgewick[1]即3。- 分组与排序:
- 算法的核心是外层的
for循环,它控制着增量 d 的变化,从选定的初始增量开始,依次使用序列中的下一个增量,直到增量变为1。phpfor ($d = $sedgewick[$si]; $d > 0; $d = $sedgewick[++$si])- 插入排序过程:
- 内层的两个
for循环实现了对每个分组的插入排序。phpfor ($p = $d; $p < $n; $p++) { // 遍历当前分组的所有元素
$tmp = $arr[$p]; // 取出待插入的元素
for ($i = $p; $i >= $d && $arr[$i - $d] > $tmp; $i -= $d) { // 在已排序部分找到插入位置
$arr[$i] = $arr[$i - $d]; // 元素后移
}
$arr[$i] = $tmp; // 插入元素
}以
[5, 4, 3, 2, 1]为例的执行过程
- 初始化:
- 数组:
[5, 4, 3, 2, 1]$n = 5$sedgewick = [5, 3, 1]- 调整初始增量:
$si从0开始,检查$sedgewick[0](5) >=$n(5),条件成立,$si变为1。所以初始增量$d = $sedgewick[1] = 3。- 第一轮排序 (d=3):
- 分组:
- 组1 (下标 0, 3):
[5, 2]- 组2 (下标 1, 4):
[4, 1]- 组3 (下标 2):
[3](只有一个元素,无需排序)- 对组1进行插入排序: 比较并交换 5 和 2,数组变为
[2, 4, 3, 5, 1]。- 对组2进行插入排序: 比较并交换 4 和 1,数组变为
[2, 1, 3, 5, 4]。- 第一轮后数组:
[2, 1, 3, 5, 4]。可以看到,元素已经比原来更接近有序了。- 第二轮排序 (d=1):
- 增量变为
$sedgewick[2] = 1。- 分组: 整个数组为一组
[2, 1, 3, 5, 4]。- 对整个数组进行直接插入排序。
- 这一步就是标准的插入排序过程,将数组最终变为
[1, 2, 3, 4, 5]。- 结束:
- 增量变为
$sedgewick[3](不存在,循环结束)。- 输出排序后的数组:
1, 2, 3, 4, 5。总结
希尔排序通过设置间隔(增量)将数组分组,对每组进行插入排序,随着增量逐渐减小,数组逐渐变得有序,最终当增量为1时进行一次插入排序即可完成整个排序。这种分组策略有效减少了数据移动的次数,提高了排序效率,尤其是在数据量较大且初始状态较为无序的情况下。
开源达人写希尔排序demo:
<?php/*** 希尔排序演示* 使用Sedgewick增量序列实现希尔排序算法*//*** 希尔排序函数** 算法原理:* 1. 选择一个增量序列,本例使用Sedgewick序列 [5, 3, 1]* 2. 按照增量序列从大到小的顺序进行排序* 3. 每一轮排序时,将数组按照增量大小分组,对每组进行直接插入排序* 4. 当增量为1时,进行最后一次直接插入排序,完成整个排序过程** @param array $arr 待排序的数组* @return array 排序后的数组*/function shellSort($arr) {$n = count($arr);$sedgewick = [5, 3, 1]; // Sedgewick增量序列echo “原始数组: ” . implode(‘, ‘, $arr) . “\n”;// 调整初始增量值,确保不超过数组长度$si = 0;while ($si < count($sedgewick) && $sedgewick[$si] >= $n) {$si++;}// 按照Sedgewick序列进行分组排序for ($d = $sedgewick[$si]; $d > 0; $d = $sedgewick[++$si]) {echo “当前增量: $d\n”;// 对每个分组执行插入排序for ($p = $d; $p < $n; $p++) {$tmp = $arr[$p];$i = $p;// 在当前分组内执行插入排序while ($i >= $d && $arr[$i – $d] > $tmp) {$arr[$i] = $arr[$i – $d];$i -= $d;}$arr[$i] = $tmp;}echo “增量$d排序后: ” . implode(‘, ‘, $arr) . “\n”;}return $arr;}// 测试数据$numbers = [49, 38, 65, 97, 76, 13, 27, 49];echo “=================希尔排序演示=================\n”;// 执行希尔排序$sortedNumbers = shellSort($numbers);echo “最终排序结果: ” . implode(‘, ‘, $sortedNumbers) . “\n”;echo “=============================================\n”;/*** 另一个更通用的希尔排序实现* 使用Knuth序列作为增量序列 (3^k – 1) / 2*/function shellSortKnuth($arr) {$n = count($arr);// 计算Knuth序列的最大增量$gap = 1;while ($gap < $n / 3) {$gap = $gap * 3 + 1; // 1, 4, 13, 40, 121, …}echo “使用Knuth增量序列进行排序:\n”;echo “原始数组: ” . implode(‘, ‘, $arr) . “\n”;// 不断缩小增量,直到为1while ($gap >= 1) {echo “当前增量: $gap\n”;// 对每个分组执行插入排序for ($i = $gap; $i < $n; $i++) {$temp = $arr[$i];$j = $i;// 在当前分组内执行插入排序while ($j >= $gap && $arr[$j – $gap] > $temp) {$arr[$j] = $arr[$j – $gap];$j -= $gap;}$arr[$j] = $temp;}echo “增量$gap排序后: ” . implode(‘, ‘, $arr) . “\n”;$gap = (int)(($gap – 1) / 3); // 缩小增量}return $arr;}// 使用Knuth序列的希尔排序测试echo “\n==============Knuth序列希尔排序==============\n”;$numbers2 = [49, 38, 65, 97, 76, 13, 27, 49];$sortedNumbers2 = shellSortKnuth($numbers2);echo “最终排序结果: ” . implode(‘, ‘, $sortedNumbers2) . “\n”;echo “=============================================\n”;?>这个希尔排序演示程序包含以下特点:详细注释:每个关键步骤都有清晰的注释说明过程可视化:在排序过程中输出每一步的结果,便于理解算法执行过程两种实现:第一种使用Sedgewick序列 [5, 3, 1]第二种使用更通用的Knuth序列 (3^k – 1) / 2清晰输出:显示原始数组、每轮增量排序后的结果和最终排序结果当你运行这个程序时,会看到类似以下的输出:=================希尔排序演示=================原始数组: 49, 38, 65, 97, 76, 13, 27, 49当前增量: 5增量5排序后: 13, 38, 65, 97, 76, 49, 27, 49当前增量: 3增量3排序后: 13, 38, 27, 97, 76, 49, 65, 49当前增量: 1增量1排序后: 13, 27, 38, 49, 49, 65, 76, 97最终排序结果: 13, 27, 38, 49, 49, 65, 76, 97=============================================这个演示可以帮助你更好地理解希尔排序的工作原理和执行过程。
再总结一翻,希望有更深的认识:<?php希尔排序的基本概念希尔排序是插入排序的改进版本。它的核心思想是:先让相距较远的元素进行比较和交换,使数组”基本有序”再逐步缩小间隔,最终进行一次普通的插入排序代码执行过程详解让我们以数组 [49, 38, 65, 97, 76, 13, 27, 49] 为例,逐步分析:1. 初始化阶段php$n = count($arr); // $n = 8 (数组长度)$sedgewick = [5, 3, 1]; // 增量序列2. 调整初始增量php$si = 0;while ($si < count($sedgewick) && $sedgewick[$si] >= $n) {$si++;}这个循环是为了确保初始增量小于数组长度:$sedgewick[0] = 5,5 < 8,所以循环不执行$si 保持为 0初始增量 $d = $sedgewick[$si] = $sedgewick[0] = 53. 第一轮排序(增量为5)php$d = 5;现在按照增量5进行分组,即每隔5个元素分为一组:索引: 0 1 2 3 4 5 6 7元素: 49 38 65 97 76 13 27 49分组: [0]———-[5][1]———-[6][2]———-[7][3][4]实际分组为:组1(索引0,5): [49, 13]组2(索引1,6): [38, 27]组3(索引2,7): [65, 49]组4(索引3): [97] (只有一个元素)组5(索引4): [76] (只有一个元素)对每组进行插入排序:处理索引5的元素13:与索引0的元素49比较,13 < 49,交换位置结果:[13, 38, 65, 97, 76, 49, 27, 49]处理索引6的元素27:与索引1的元素38比较,27 < 38,交换位置结果:[13, 27, 65, 97, 76, 49, 38, 49]处理索引7的元素49:与索引2的元素65比较,49 < 65,交换位置结果:[13, 27, 49, 97, 76, 49, 38, 65]第一轮排序后数组变为:[13, 27, 49, 97, 76, 49, 38, 65]4. 第二轮排序(增量为3)php$d = 3;按照增量3分组:索引: 0 1 2 3 4 5 6 7元素: 13 27 49 97 76 49 38 65分组: [0]——–[3]——–[6][1]——–[4]——–[7][2]——–[5]实际分组为:组1(索引0,3,6): [13, 97, 38]组2(索引1,4,7): [27, 76, 65]组3(索引2,5): [49, 49]对每组进行插入排序:组1排序后: [13, 38, 97] 组2排序后: [27, 65, 76] 组3排序后: [49, 49]第二轮排序后数组变为:[13, 27, 49, 38, 65, 49, 97, 76]5. 第三轮排序(增量为1)php$d = 1;增量为1时,就是普通的插入排序,对整个数组进行排序:最终结果:[13, 27, 38, 49, 49, 65, 76, 97]核心代码解释php// 外层循环控制增量序列for ($d = $sedgewick[$si]; $d > 0; $d = $sedgewick[++$si]) {// 中层循环从第d个元素开始,到数组末尾for ($p = $d; $p < $n; $p++) {$tmp = $arr[$p]; // 取出当前元素$i = $p;// 内层循环进行插入排序// 在当前分组中向前比较,如果前面的元素大于当前元素,则向前移动while ($i >= $d && $arr[$i – $d] > $tmp) {$arr[$i] = $arr[$i – $d]; // 元素向后移动$i -= $d; // 继续向前比较同一分组的元素}$arr[$i] = $tmp; // 将当前元素插入到正确位置}}为什么希尔排序更高效?减少数据移动:通过大增量的排序,使数组快速接近有序状态降低比较次数:当进行最后的插入排序时,数组已经基本有序,大大减少了元素比较和移动的次数时间复杂度优化:相比O(n²)的插入排序,希尔排序的时间复杂度约为O(n^1.3)希望这样详细的解释能帮助你理解希尔排序的工作原理!
总结
排序的入门餐怎么样?我们可不是直接就拿烂大街的冒泡和快排上手的吧。不出名不意味着不会用到,比如我面试的时候曾经有个公司就是在面试题上写明了不能使用冒泡和快排。这时候,我相信简单插入排序直观好理解的特性一定就能帮助我们度过这种面试难关了哦!